- * Les auteurs tiennent à remercier Yvette Grelet, ingénieur de recherche au CEREQ, et Marie Cottrell (...)
1L’objet de cet article est d’illustrer l’intérêt de l’utilisation des cartes d’auto-organisation dans un but de classification, à travers divers exemples et approches. La diversité des exemples du point de vue des domaines d’application (biométrie, économie, énergie) et de la problématique statistique (typologie, classification de séries chronologiques ou de courbes) permet de mettre en avant différentes propriétés caractéristiques des cartes d’auto-organisation en référence à des méthodes plus classiques. L’exemple en biométrie sur l’aspect de la peau du visage sera utilisé tout au long de l’article pour présenter la technique, tandis que d’autres exemples sur la structuration de l’offre de formation, les parcours professionnels, les profils de courbes de la consommation électrique nationale polonaise, illustreront ses possibilités graphiques et d’analyse. Il n’est, bien sûr, pas question de présenter cette technique comme supérieure aux autres, cependant dans chaque exemple traité, l’accent sera mis sur l’apport particulier de cette méthode par rapport à des méthodes plus traditionnelles que l’on pourra trouver dans Lebart et al. (1995).
2L’algorithme d’auto-organisation est présenté aujourd’hui en statistique comme une généralisation qui introduit une notion de voisinage entre les classes de l’algorithme des centres mobiles. Cette propriété est traduite par une carte qui organise les classes selon leur proximité. Dans un premier temps, cette carte sera présentée comme un support graphique d’analyse du résultat de la classification en mettant en avant la variété des représentations possibles. Certaines sont plutôt performantes pour synthétiser un résultat (en particulier, pour visualiser les effets de variables endogènes ou exogènes, qualitatives ou quantitatives), d’autres proposent une représentation des individus adaptée à leurs caractéristiques (par exemple, des courbes pour des données temporelles). Dans un second temps, cette carte sera utilisée comme représentation d’une surface susceptible d’épouser au mieux le nuage de points. Dans ce cas, on peut, au choix, utiliser la carte comme complément à la classification conjointe, ou l’en déconnecter, et considérer la surface comme un ajustement de la structure des données sur laquelle on peut projeter le résultat d’une classification éventuellement issue d’une autre méthode que celle liée à l’algorithme, ou toute sorte d’information.
3Le couplage de la classification et d’une représentation de la structure intrinsèque des données est l’aspect original de cette technique qui permet souvent de « voir autrement les données » qu’en ayant recours aux méthodes classiques. Par exemple, l’analyse factorielle visualise les données par des projections planes qui traduisent la décomposition en facteurs principaux. Ce mode de représentation, familier aux utilisateurs, rendent bien compte des grandes distances entre les individus, et moins bien des éventuels effets des facteurs de moindre contribution. Dans certains cas, ces effets sont mineurs, du point de vue de la population globale, mais sont déterminants pour expliquer la différence entre deux sous-populations voisines ; on parle alors d’un effet local. De leur côté, les algorithmes de classification prennent en compte à la fois les effets des grandes distances et les effets locaux. Contrairement aux cartes d’auto-organisation, les techniques de classification n’ont pas de système de représentation graphique associé. En général, on couple une classification avec une analyse factorielle pour en représenter le résultat, ce qui a pour conséquence de visualiser plutôt la prise en compte des grandes distances par la classification que celle des effets locaux. Dans ce contexte, les cartes d’auto-organisation se rapprochent du couple « analyse factorielle-classification » en optimisant la représentation de la classification ; c’est-à-dire, en rendant compte à la fois des effets des grandes distances et des effets locaux.
4Cette méthode s’intègre très bien dans l’évolution de la statistique qui doit s’adapter à des bases de données de plus en plus grandes en termes d’individus enquêtés et de questions posées, et doit fournir des solutions en termes de visualisation et de synthèse. Dépasser les trois ou quatre dimensions principales, pouvoir travailler sur de grandes tendances au lieu des axes principaux (par exemple, en révélant des mouvements non-linéaires), ou percevoir des nuances de comportement chez certaines sous-populations, sont des objectifs de plus en plus fréquents.
5La première partie de cet article présentera l’algorithme en mettant l’accent sur les points nécessaires à l’utilisateur ; c’est-à-dire, sur la notion de voisinage et la lecture de la carte (la partie algorithmique proprement dite n’est pas traitée). Dans une deuxième partie, nous montrerons une large variété de représentations graphiques qu’offre la carte, d’abord pour l’analyse de la classification associée, et comme visualisation de la structure intrinsèque des données. Enfin, dans la dernière partie, nous comparerons les cartes d’auto-organisation au couple « analyse factorielle-classification » en mettant l’accent sur ses points forts : la complémentarité entre visualisation et classification, et son adaptabilité aux structures de données non linéaires.
6Les cartes d’auto-organisation, qui utilisent l’algorithme non supervisé de Kohonen (Kohonen (1995), Cottrell et al. (2003)), ont souvent été utilisées en analyse des données (Blayo et Demartines (1991), Oja et Kaski (1999)). Nous allons, dans cette partie, présenter sommairement la technique pour fournir à un utilisateur les moyens de comprendre son fonctionnement sans entrer dans le détail de l’algorithme. L’exemple qui va nous servir à illustrer la présentation de la méthode est une typologie de la peau du visage établie par le CERIES à partir des données de 212 femmes selon la présence ou l’absence de 17 critères visuels comme l’aspect gras de la peau ou de critères tactiles comme la rugosité au touché. La distance utilisée dans cette étude est la distance euclidienne (on aurait pu choisir celle du χ2 mais nous désirions pouvoir généraliser la méthode à un relevé d’intensité d’apparition du critère au lieu de sa seule présence). Cette base de données a un grand nombre de variables et relativement peu d’individus, ce qui donne beaucoup de souplesse à la structure des données et a rendu cet exemple très intéressant pour mettre en évidence les propriétés d’ajustement des cartes d’auto-organisation.
7La méthode de classification à l’aide des cartes d’auto-organisation appartient à la famille des algorithmes conduisant à des partitions comme les méthodes d’agrégation autour des centres mobiles ou de nuages dynamiques (Lebart (1995)). Il est d’ailleurs identique dans sa phase finale, dite à zéro-voisin, à l’algorithme de Forgy dans sa version stochastique (Forgy (1965)). Cette méthode en a un certain nombre de caractéristiques : le nombre de classes est fixé par l’utilisateur, et elle est adaptée aux données de grande taille. Son originalité est d’introduire une notion de voisinage entre les classes et d’utiliser un support graphique associé, appelé « carte », qui organise les classes en fonction de leur voisinage. C’est cet aspect que nous allons développer.
8La carte est un réseau dont le nombre d’unités et la structure sont choisis par l’utilisateur. Chaque unité est représentée par un rectangle qui symbolise une classe. Les structures les plus usuelles sont la ficelle (figure 1a) et la grille (figure 1b), mais on trouvera dans l’exemple sur la consommation électrique nationale polonaise une structure en cylindre (figure 1c) qui n’est autre qu’une grille dont les côtés latéraux se rejoignent. La ficelle est généralement utilisée lorsque l’on désire faire apparaître un ordre entre les classes, alors que la grille met en valeur des liaisons intra-classes multidimensionnelles. En général, le choix d’une autre structure est guidé par une particularité des données. Dans l’exemple où la structure en cylindre a été préférée à la grille, la raison était de prendre en compte à la fois le cycle des mois (le mois de décembre rejoint celui de janvier à la fois du point de vue du calendrier et de la consommation électrique), et la rupture hebdomadaire entre la consommation électrique du week-end et celle de la semaine ouvrée.
Figure 1 : Différentes structures pour la carte d’auto-organisation


Dans la structure « en ficelle » (figure 1a), les unités sont alignées. La structure « en grille » (figure 1b) a deux dimensions, la numérotation est faite de gauche à droite et de haut-en bas. La structure « en cylindre » (figure 1c) est, elle, une structure en grille dont deux bords se rejoignent.
9La notion de voisinage est induite par la structure de la carte (c’est donc un choix a priori). Sont considérées comme voisines, les unités proches sur la carte (cf. ci-après). Le résultat de l’algorithme est d’affecter à chaque unité un vecteur de l’espace des données appelé « vecteur code ». A chaque individu de l’espace des données, on attribue l’unité dont le vecteur code est le plus proche. On constitue ainsi une classification. Le vecteur code de l’unité u converge vers le centre de la classe associée (le barycentre des individus de la classe), on les confondra dans la suite. La propriété majeure de l’algorithme est que deux individus associés à des classes, dont les unités sont voisines sur la carte, sont voisins dans l’espace des données au sens de la distance choisie (dans le cas de l’exemple sur la peau du visage humaine, la distance euclidienne). Sur la figure 2, les unités voisines de celle numérotée 24 sont, au rayon 1, les unités grisées en foncé qui l’entourent, plus elle-même (16, 17, 18, 23, 24, 25, 30, 31 et 32) alors qu’au rayon 0 c’est elle-même, et au rayon 2 ce sont les unités précitées plus celles grisées en clair qui les entourent (8 à 12, 15, 19, 22, 26, 29, 33 et 36 à 40). En conséquence, les femmes affectées aux classes dont les unités sont 24 et 25 et qu’on appellera dans la suite les classes 24 et 25, présentent des caractéristiques de peau du visage voisines.
Figure 2 : Les unités voisines de la classe 24 gris foncé au rayon 1 sont les unités gris foncé (16, 17, 18, 23, 24, 25, 30, 31 et 32), au rayon 2 s’ajoutent celles grisées en clair (8, 9, 10, 11, 12, 15, 19, 22, 26, 29, 33, 36, 37, 38, 39 et 40)

Les individus associés à des classes voisines sont proches dans l’espace des données. Les femmes des classes 24 et 25 présentent donc une peau du visage ayant des caractéristiques similaires.
10Nous ne présentons pas ici la théorie concernant l’algorithme, signalons toutefois que sa convergence n’a été pour l’instant prouvée que dans un cadre restreint (Bénaim et al. (1998). Un contrôle de la stabilité de la structure de la carte par une relance multiple à l’aide de bootstraps reste possible, son utilisation sur plusieurs exemples a conclu en faveur des cartes d’auto-organisation dans la mesure où les individus voisins le sont avec une répétition significative d’une proximité dans l’espace des données (Benaim et al. (1998), Cottrell et al. (1998)).
11Les unités de la carte, matérialisées par des rectangles, sont considérées comme des fenêtres graphiques. Elles permettent de représenter l’information désirée sur toutes les classes simultanément (Rousset (1999), Cotrell et Rousset (1997)). On peut ainsi lister le nom des individus de chaque classe comme en analyse en composante principale, donner une liste de propriétés comme dans l’exemple de la structuration de l’offre de formation présenté plus loin, y inscrire un tableau de fréquence, ou représenter une dimension qualitative par un camembert ou un histogramme, représenter une série de « box-plots » dans le cas de données quantitatives, ou encore tracer des courbes comme nous le verrons dans l’exemple sur les parcours professionnels. Le grand avantage de cette représentation provient de l’organisation des unités ; c’est-à-dire, des fenêtres par voisinage. Elle permet de traiter ensemble les classes voisines qui ont une caractéristique commune. On parle alors de la caractéristique d’une région de la carte (zone connexe de la carte). De la même façon, elle indique qu’une caractéristique est partagée par deux populations, par ailleurs globalement différentes, lorsqu’elle se retrouve sur deux régions éloignées sur la carte. L’analyse par régions de voisinage permet de traiter une grande partie de la redondance. En effet, dès l’instant où deux classes sont voisines, on s’attend à ce qu’elles aient un grand nombre de caractéristiques communes du point de vue des variables endogènes et exogènes. L’ensemble des caractéristiques communes s’interprète, alors, ensemble par le fait que l’on a deux populations d’individus très proches. Cette méthode met en évidence des effets locaux (entre classes voisines); c’est-à-dire, les dimensions qui éloignent ou rapprochent des classes voisines. Cette propriété est d’autant plus intéressante que l’effet des petites distances est mal rendu par l’analyse factorielle. Dans l’exemple de l’étude sur l’aspect de la peau du visage (figure 3), on a représenté la part de la présence du critère « peau plutôt jaune » dans chaque classe. On y perçoit quatre régions de la carte : en haut-gauche (unités 1, 2 et 8) et en bas-droite (28, 34, 35, 41, 42, 46 et 49) où on trouve les régions typées « peau plutôt jaune », en haut-droite (7, 14 et 21) où se trouve une région mixte, et le reste de la carte qui est typé « peau non jaune ».
Figure 3 : Cartographie d'une variable qualitative

Dans l’exemple sur l’aspect de la peau, la couleur foncée indique que le critère « peau plutôt jaune » est présent. Dans l'unité 14, 25% des individus ont la "peau plutôt jaune". Dans 2 régions le caractère domine : L’angle en haut à gauche, l’angle en bas à droite. La région haut-droite est mixte. Ailleurs, ce critère est absent.
12La carte est une représentation symbolique des classes qui les répartit de façon régulière alors que ce n’est pas un quadrillage régulier de l’espace des données : la distance entre les classes dans cet espace varie comme dans toute classification. Le nombre des unités pouvant être important, il arrive souvent d’avoir besoin d’un second niveau de résumé. Nous proposons de regrouper les unités de la carte en régions de proximité à l’aide d’une classification hiérarchique ascendante sur leurs centres de classes. Les nouvelles classes sont appelées macro-classes bien que, ayant choisi de ne pas pondérer les centres de classes par leurs effectifs, ce soit une proximité dans l’espace qui est décrite, et non un deuxième niveau de classification des individus (comme dans un couple « centres mobiles - classification hiérarchique »). Les fenêtres graphiques permettent évidemment de superposer plusieurs informations, et nous avons l’habitude d’utiliser la couleur de fond pour indiquer à quelle macro-classe le centre de classe appartient. Dans l’exemple sur l’aspect de la peau du visage (figure 4), on distingue six macro-classes. Les régions décrites précédemment « en haut à gauche » et « en bas à droite » (étendue de la classe 27) correspondent à deux macro-classes, la région « en haut à droite » appartient, quand à elle, à une macro-classe plus large, alors que la région « peau non jaune » est divisée en trois macro-classes.
Figure 4 : Carte d’auto-organisation avec 2 niveaux de regroupement

Une classification hiérarchique réalisée sur les centres de classes aboutit à 6 macro-classes indiquées par le niveau de gris du fond des cellules.
13Dans cette partie nous allons présenter trois exemples de typologies : la consommation électrique journalière nationale polonaise, la structure de l’offre de formation réalisée à partir d’une enquête menée par le CEREQ auprès des organismes de formation continue, et les parcours professionnels tirés de l’enquête « Génération 92 » du CEREQ. Le premier exemple utilise la distance euclidienne, le deuxième celle du χ2, et le troisième une distance construite. Le premier et le troisième sont des exemples de classements de courbes.
14Cet exemple se situe dans le contexte d’une étude plus large dont l’objectif était de prévoir la consommation électrique horaire du lendemain à partir d’un relevé de la consommation horaire nationale d’électricité en Pologne du 01 janvier 1986 au 31 décembre 1993 (Rousset (1999), Cottrell et al. (1998) et Rousset (2000)). La figure 5, qui représente le tracé du suivi horaire sur trois exemples de jours, illustre la diversité de ces relevés. La consommation horaire est expliquée essentiellement par trois facteurs : la température, l’activité économique (essentiellement pendant les heures de travail) et l’activité domestique et de loisir (essentiellement durant la soirée). La température ayant essentiellement un impact en termes de niveau de consommation électrique (moyenne journalière) et d’amplitude (écart type), alors que l’activité économique et l’activité domestique et de loisir se retrouvent dans le profil journalier, qui n’est autre que le vecteur des 24 relevés horaires que l’on a réduit de l’écart type journalier, après leur avoir soustrait la moyenne journalière. La méthode de prévision a consisté à prévoir globalement le profil de consommation journalier à partir de la classification dont nous présentons ici le résultat, et à prédire séparément avec un modèle ARIMA ou avec un perceptron multicouche la moyenne et l’écart type. Son résultat est présenté sur la figure 6.
Figure 5 : Exemple de la consommation horaire électrique nationale polonaise: trois exemples de jours montrent trois profils de consommation différents

Le dimanche 01 mars 1987, la pointe est due à l'activité domestique et au chauffage.

Le lundi 02 mars 1987, la première poussée de consommation est due au chauffage et à l'activité économique, la pointe du soir à l'activité domestique et au chauffage.

Le lundi 08 août 1988, la première hausse est due à l'activité économique et le pic du soir à l'activité domestique.
Figure 6 : Exemple de la consommation horaire électrique nationale polonaise - représentation des profils de consommation

Superposition du tracé de tous les individus de chaque classe : les représentations des 2922 profils de consommation électrique nationale polonaise sont superposés dans leur unité d'affectation, l’épaisseur de la superposition des traits donnant un aperçu de l’homogénéité de chaque classe.

Tracé de la courbe moyenne de chaque classe : dans chaque case est tracé la solution de l’algorithme (vecteur code) associé à l’unité qui a convergé vers le profil de consommation électrique moyen de la classe, c’est le représentatnt de la classe. Dans le cas d’une classe vide, c’est un barycentre des représentants des classes voisines.
15La classification utilise une carte d’auto-organisation dont la structure est cylindrique ainsi que nous l’avons expliqué précédemment. Sur la figure 6a est tracé chaque profil dans la fenêtre attribuée à sa classe; c’est-à-dire, les 24 valeurs successives d’une même journée reliées entre elles. Cette représentation des 2922 jours donne un aperçu d’une certaine variabilité intra classe : plus l’épaisseur de la superposition des traits est fine, plus la classe est homogène. La figure 6b montre le centre de classe : deux profils voisins ont des formes similaires (l’unité d’un bord latéral est voisine de celle du bord opposé dans le cas d’une carte cylindrique). La structure de voisinage de la carte rend donc bien compte de la proximité des profils de consommation électrique dans l’espace. Sur la figure 7a, on a choisi de représenter par un camembert la part du type de jour de semaine dans chaque classe. Les dimanches et les jours fériés se retrouvent en zone centrale, encerclés des samedis et des ponts, les autres, les jours ouvrés, occupent le reste de la carte de façon assez homogène, avec l’apparition d’une particularité pour les lundis. Lorsque l’on fait de même avec les mois (figure 7b), on voit pour la zone des jours ouvrés le suivi temporel se dessiner sur la carte avec une rupture au moment du changement horaire (le suivi des mois d’été est présenté dans l’ouvrage Rousset (1999)). On observe le même phénomène pour les dimanches en zone centrale. La propriété qui est ressortie de ces cartes d’auto-organisation est la possibilité, à partir des variables calendaires d’un jour, de prévoir une région de la carte restreinte à laquelle appartient son profil (et ceci quelle que soit l’échéance de prévision). Cette propriété a permis de définir deux méthodes de prévision de la consommation électrique journalière : la première reposant sur une approche bayésienne et de série chronologique (de type ARIMA ou perceptron multicouche) Rousset (1999), Cottrell et al. (1998); la seconde, plus dynamique, de type markovien fournit pour chaque classe la carte de prévision du lendemain (qui ne dépend pas du temps), et ensuite utilise celle attribuée à la classe du jour t pour prévoir le profil du jour t+1 (Rousset (2000)).
Figure 7 : Cartographie des jours de semaines et mois

La figure 7a représente la cartographie des jours de semaine codés sous 4 modalités : les lundis, les jours du mardi au vendredi, les samedis et les dimanches. Dans les classes du centre de la carte (intérieur de l’ellipse interne) sont regroupés les dimanches et les jours fériés. Au contraire, dans les classes situées à l’extérieur de l’ellipse externe on trouve les jours ouvrés. Les samedis sont situés sur la zone tampon correspondant à la zone comprise entre les deux ellipses. Durant cette période, certains samedis étant travaillés en Pologne, la frontière entre les samedis et les jours ouvrés est moins nette qu’entre les samedis et les dimanches.

La figure 7b représente la cartographie des mois. Dès l’instant où l’on a fixé un type de jour de semaine (par exemple les dimanches ou les jours ouvrés) , on constate que l’évolution du cycle annuel des mois explique à la fois la structure intra-classes et inter-classes. En effet, les classes regroupent au plus trois mois consécutifs et partagent au moins un mois avec leurs voisines.

Sur la figure 7c, on a localisé les zones de la carte où apparaissent les mois d’hiver pour respectivement les jours ouvrés et les dimanches. On constate alors un ordonnancement suivant le cycle des mois (la carte étant un cylindre, les bords latéraux sont en réalité contigus).
16Dans cet exemple (Vero et Rousset (2003 a et b)), 428 organismes de formation décrivent 1200 pôles de compétences à travers huit dimensions, elles-mêmes détaillées en items. Sans énoncer les différents items, les dimensions à sélectionner éventuellement sont : « une spécialité de formation » (l’item est alors une spécialité), « un public particulier », « un diplôme ou un titre préparé », « un type de financeur ou client spécifique », « une modalité particulière de formation » (alternance, FEST, ...), « un niveau de formation visé », « une offre de services complémentaire à la formation », et enfin « un territoire particulier ». L’individu est le pôle et les variables sont les items des dimensions. La distance choisie est la distance du χ2. La figure 8 montre la carte d’auto-organisation résultante. Les 10 macro-classes constituent des zones connexes de la carte; elles sont délimitées par un trait continu (la couleur du fond aide aussi à les distinguer). Leurs caractéristiques sont écrites en clair sur fond gris foncé. Au niveau des classes est énoncée en noir la liste des items qui dominent (autres que ceux communs à la macro-classe). Cette description montre les dimensions qui fédèrent les macro-classes (écrites en clair), et celles (écrites en foncé) qui créent des effets locaux, ou qui définissent d’éventuelles passerelles entre les classes. Ainsi la macro-classe 1 regroupe les pôles de compétences destinés aux demandeurs d’emploi et assortis d’un financement public. Parmi les classes de la macro-classe 1, les pôles de compétences de la classe 2 délivrent, en plus, des diplômes d’état, propriété qui se retrouve dans la classe 3 voisine (laquelle appartient à la macro-classe 2 identifiée principalement par la spécialité de formation des « services aux personnes et à la collectivité »). Les cases vides correspondent effectivement à des classes vides ou de faibles effectifs qui n’ont pas pu être définies. Dans les autres exemples, les sorties graphiques ont été automatisées, mais la figure 8 représente la synthèse de plusieurs de ces cartes en une seule. Cet exemple illustre la raison pour laquelle la carte est un aussi bon support pour confronter le mécanisme d’agrégation de l’algorithme avec les connaissances a priori du domaine d’application, dans la mesure où l’on peut contrôler si les liens de voisinage, traduits par des items de dimensions communes et qui sont ceux qui ont rapproché ces classes, correspondent effectivement à une réalité économique ou non.
Figure 8 : Structuration de l’offre de formation - une cartographie des pôles de compétence - dix macro-classes de formation (macro-pôles) agrègent 36 classes (micro-pôles)

Les caractéristiques des macro-pôles, respectivement micro-pôles, sont listées en clair, respectivement en noir. La carte décrit simultanément deux niveaux d’agrégation des pôles et les liens entre les classes résultantes (les traits plus épais indiquant des liens moins tenus). Les cases vides correspondent à des classes vides ou de faible effectif (moins de 5% en cumulé) difficiles à analyser.
17Dans cet exemple, on a extrait de l’enquête « génération 92 » 2422 parcours de jeunes femmes sorties du système scolaire au niveau du baccalauréat. Les variables sont chronologiques, et représentent la situation mensuelle des 57 mois consécutifs compris entre juillet 1992 et avril 1997. La valeur de la variable est un code de situation parmi sept états possibles (« le CDI », « le CDD », « le CES », « le contrat de qualification ou d’apprentissage », « le chômage », « l’inactivité », et enfin « la formation ou étude »). La distance entre les trajectoires a été construite afin de prendre en compte l’écart entre les différents états du marché du travail (l’écart entre un « CDI » et un « contrat d’apprentissage » n’étant pas le même qu’entre un « CDI » et « l’inactivité »). Nous avons choisi de quantifier cet écart par une mesure du coût de passage par l’état pour atteindre le CDI, mesuré en mois : deux états qui constituent un tremplin vers le CDI sont proches et, au contraire, distants d’un état qui maintient l’individu dans une situation de transit. Plusieurs représentations ont été proposées pour caractériser les classes (Grelet (2002)) parmi lesquelles nous avons sélectionné la fréquence d’apparition de chaque état pour chacun des 57 mois. La figure 9a montre une classe où, dans les premiers mois, environ 50% des individus sont en « CDD », 25% en « CDI » et 25% au « chômage », et, dans les derniers mois, 100% ont obtenu un « CDI » alors que les états « CES » et « contrat de qualification ou apprentissage » n’apparaissent jamais. Cette représentation montre bien quels sont les états concernés pour chaque période, mais perd la structure en trajectoires sous-jacentes : en effet, deux états peuvent apparaître à des périodes consécutives sans qu’ils existent sur une même trajectoire. Sur la figure 9b, toutes les classes sont représentées grâce au type de graphique précédemment décrit. L’organisation sur la carte rapproche des trajectoires similaires mais décalées dans le temps. On y perçoit deux mouvements qui correspondent à des évolutions temporelles par rapport à l’état « CDI » :dans le premier mouvement, le « CDI » est obtenu de plus en plus tardivement, alors que le second correspond à une perte ou un abandon de « CDI ». Le premier mouvement passe du « CDI immédiat » au « CDD suivi de CDI », puis au « contrat de qualification suivi de CDI », puis au « contrat de qualification suivi de CDD puis CDI » et enfin au « CES et chômage ».
Figure 9 : Cartographie des parcours professionnels
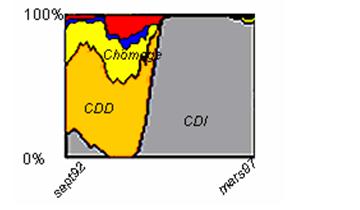
La figure 9a représente Ecoulement mensuel de la cohorte des jeunes femmes entre les différents états CDI, CDD, CES, Contrat de qualification, chômage, inactivité, formation études.

La figure 9b est une cartographie des parcours professionnels où l’évolution temporelle apparaît sur la carte. Par exemple, une tendance apparaît dans l’organisation des classes en fonction du délai d’obtention d’un CDI : d’abord rapide, ensuite retardé par le passage à un CDD puis plus tardif lorsqu’un contrat de qualification sert de tremplin et enfin pas d’obtention de CDI.
18Le couple « analyse factorielle-classification » (Wong (1982)) associe deux algorithmes différents, et non un même algorithme à deux facettes, comme pour la carte d’auto-organisation. L’analyse factorielle est employée dans ce cadre pour fournir une représentation graphique par projection sur des plans construits à partir des 3 ou 4 axes principaux. La qualité majeure en terme de visualisation de cet outil, en plus de sa simplicité d’usage, est d’exploiter au mieux le support graphique qu’est l’écran ou la feuille de papier. Il n’est en revanche pas conçu pour optimiser la représentation d’une classification, en particulier lorsque les effets cumulés des axes secondaires l’ont influencée, car il y a alors un phénomène bien connu d’écrasement des projections. Il est à noter que dans un contexte d’augmentation permanent de la taille des données en termes de variables et d’individus, les méthodes statistiques doivent désormais répondre à un intérêt croissant vis-à-vis des dimensions secondaires, les effets des dimensions primaires étant souvent déjà connus. De son côté, la carte d’auto-organisation représente au mieux la classification et, dans le même temps, la classification agrège les individus en prenant en compte la structure de la carte. Elle peut être utilisée pour représenter la structure des données. Chaque centre de classe est alors considéré comme un point de l’espace à forte densité, relié sur la carte à ses voisins, ce qui simule la continuité dans l’espace : la carte devient alors la visualisation d’une surface qui ajusterait au mieux le nuage de points. La surface étant plus souple que le plan, elle peut mieux s’adapter aux données, et en particulier aux structures non linéaires. Par contre, la représentation est symbolique. Il est donc nécessaire d’utiliser des outils graphiques complémentaires (comme les macro-classes, ou d’autres outils comme ceux présentés dans la suite) pour comprendre la structure de la surface alors que, dans le cas de projections, la structure du plan est celle du support de travail lui-même (la feuille ou l’écran). Une comparaison plus précise se trouve dans l’ouvrage (Rousset (1999), Rousset et Guinot (2002)).
19L’exemple de l’aspect de la peau du visage est un bon support pour illustrer ce que peuvent apporter les cartes d’auto-organisation, par rapport au couple « analyse factorielle-classification », car la structure intrinsèque de ces données a des caractéristiques que l’analyse factorielle a du mal à représenter. En particulier, un grand nombre de dimensions a une contribution significative, et les données ont une structure non linéaire, partiellement en « fer à cheval », laquelle est connue pour être mal prise en compte par les projections. Cet exemple nous permettra de montrer, d’une part, comment la carte d’auto-organisation s’adapte à ce type de structures en proposant une surface qui se replie et, d’autre part, pourquoi cette carte, qui est liée dans sa construction à une classification, s’adapte à la représentation des classifications en général. Comme exemple d’application, nous utiliserons les résultats de deux classifications déjà réalisées sur cet échantillon (Chavent et al. (1999), Guinot et al. (1997)) que nous projetterons, d’une part, sur le plan principal et, d’autre part, sur la carte d’auto-organisation. Les deux méthodes de classification sont la classification hiérarchique ascendante avec la distance de Ward et une segmentation. Il est à noter que la carte est ici utilisée uniquement comme représentation graphique. Pour plus de lisibilité, dans la suite le terme « classe » fera référence à la classification hiérarchique, « segment » à la segmentation et « groupe » à la classification par la carte d’auto-organisation.
20Sur la figure 10, la projection sur le plan principal de tous les individus pointés par le symbole de leur classe sépare assez bien les différentes classes. Néanmoins, on perçoit des zones de recouvrement (cerclées) et des distances intra-classes très grandes sur le plan qui révèle un effet important d’écrasement des projections. La différence d’interprétation entre les deux classifications est illustrée par le tableau 1 qui ne se réduit pas à une diagonale, en particulier pour la classe 3 ou le groupe 2. Les figures 10b et 10c comparent la même projection des individus pointés à gauche par le code de la classification hiérarchique et à droite par celui de la segmentation. La zone centrale correspond d’un côté essentiellement à la seule classe 3, mais de l’autre à trois segments (1, 2, 4). La représentation très homogène de cette zone traduit mal son interprétation différente par les deux algorithmes. Regardons maintenant la projection de ces mêmes classifications sur la carte d’auto-organisation.
Tableau 1 : Tableau de contingence croisant les classes issues de la classification hiérarchique et de la segmentation

Les effectifs sont exprimés en pourcentage du nombre total d’individus. Ce tableau ne se réduit pas à une diagonale (le segment 3 se répartit dans les classes 1 et 4 dans des proportions de l’ordre de 1/ 3, respectivement 2/3 et la classe 3 se répartit dans les segments 1, 2 et 4). Les interprétations relatives aux deux méthodes sont donc partiellement différentes.
Figure 10 : Projection sur le même plan principal des individus pointé avec le symbole de deux classifications différentes - les figure 10a et 10b concernent la classification hiérarchique et la figure 10 c la segmentation

Les individus sont pointés par le symbole de leur classe d’appartenance. Dans la figure 10 a, on observe des zones où se recouvrent les classes et des distances entre les projections de deux individus d’une même classe très importantes.

Dans les figures 10b et 10c, La zone centrale est dans un cas interprétée comme un seul groupe et dans l’autre répartie dans 3 classes. Cette différence d’interprétation décrite par le tableau 1 n’est pas expliquée par la projection sur le plan à cause d’un effet d’écrasement.
21Pour projeter sur cette carte une classification quelconque, on peut, par exemple, effectuer un tri croisé de ses classes avec les groupes de la carte d’auto-organisation. Le tableau de contingence résultant peut se traduire par les graphiques de la figure 11. Les camemberts y traduisent le profil des éléments d’un groupe en fonction de la classification hiérarchique (l’effectif du croisement est rapporté à celui des individus du groupe), alors que les histogrammes traduisent la répartition de chaque classe dans les unités de la carte (l’effectif du croisement est alors rapporté à celui de la classe). Il est rassurant de voir que la classification est cohérente avec la carte dans la mesure où un grand nombre de groupes ne partage ses individus qu’avec une seule classe, que les individus d’une classe se répartissent en général sur des régions (zones connexes) de la carte, et que les unités mixtes coïncident avec des zones frontières entre ces régions. La carte sépare bien les classes et indique celles qui se rapprochent. De ce point de vue, elle se comporte mieux que la projection. L’exception majeure concerne la classe 3 qui se répartit sur les deux angles (haut-gauche et bas-droite) opposés de la carte. Cette apparente contradiction est due à ce que la carte simule une surface qui se replie sur elle-même, de sorte que les deux angles opposés se rapprochent.
Figure 11 : Cartographie des deux classifications (hiérarchique et segmentation)

Figure 11 a : Cartographie de la classification hiérarchique

Figure 11 b : Cartographie de la segmentation
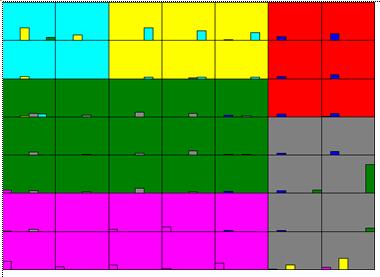
Figure 11 c : Cartographie de la classification hiérarchique.
La couleur indique le numéro de la classe dans l’ordre suivant :
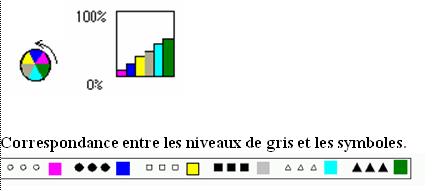
Le contingent du croisement entre les groupes de la carte d’auto-organisation et les classes (respectivement segments) de la classification hiérarchique (resp. segmentation) sont exprimés en pourcentage des effectifs des groupes dans les figures a et b , et des effectifs des classes (resp. segments) dans la figure c. Les classes correspondent en général à des zones connexes de la cartes. Les rares recouvrements sont situés aux frontières de ces zones. L’exception concerne les angles haut-gauche et bas-droite.
22La figure 12 montre la projection des représentants des groupes de l’auto-organisation sur le plan principal (de ces 49 vecteurs et non de l’ensemble des données). Les représentants sont reliés à 4 de leurs 8 voisins : en raison d’effets de surcharge, les connections entre les voisins en diagonale ne sont pas tracées. Les lignes ainsi construites génèrent une surface qui joint les différents centres de classes. Les contours de cette surface, tracés sur la figure 12 montrent le repliement de la surface. Les représentants des groupes sont pointés par le symbole de la classe hiérarchique qui y domine (on superpose deux symboles pour les groupes mixtes). Cette représentation indique que le rapprochement des deux bords a été traduit différemment par la méthode de classification hiérarchique et la méthode de segmentation. La première a eu tendance à agréger ces deux régions dans la classe 3 alors que la suivante y a décelé trois populations différentes. Cet exemple illustre dans le même temps l’inconvénient de la représentation symbolique. Il est donc nécessaire de garder la carte pour représenter la surface tout en la complétant par des outils graphiques qui permettent aussi de contrôler la structure de la surface, tels que ceux que nous présenterons dans la suite.
Figure 12 : Projection des centres de classes de la carte d’auto-organisation sur leur plan principal - chaque centre est reliés à 4 de ses 8 voisins (ceux en diagonale ne sont pas présents pour éviter une surcharge)

Figure 12 a : La carte d’auto-organisation ajuste les données par un surface qui dans l’exemple sur la qualité de la peau se replie sur elle-même - ces liens génèrent une surface dont le bord est tracé, les numéros indiquant l’unité de la carte correspondante (uniquement pour les unités du bord). La surface se replie sur elle-même.

Figure 12 b : Interprétation de la surface à partir de la classification hiérarchique - les deux bords du repliement sont regroupés les centres de classes sont pointés par le symbole de la classe hiérarchique dominante. Le repliement de la surface explique que les angles opposés de la carte (haut-gauche et bas-droite) coïncide avec la même classe hiérarchique. La classification hiérarchique regroupe les deux angles du recouvrement alors que la segmentation les séparent.
23La représentation symbolique par la carte d’auto-organisation dispose les unités de façon régulière, ce qui traduit mal la distorsion du nuage de points comme nous venons de le voir dans l’application précédente. Nous présentons dans ce paragraphe deux outils graphiques, en plus des macro-classes, pour rendre compte de la structure intrinsèque des données. Le premier outil (figure 13) représente la distance entre classes voisines, et le suivant (figures 14 et 15) représente la matrice des distances inter-classes.
Figure 13 : Carte des distances entres classes voisines - l’épaisseur du blanc entre deux unités est proportionnel à la distance entre les classes

Figure 14 : Distance entre la classe 1 et toutes les autres - la distance est d’autant plus grande que la couleur est sombre. On constate que les deux angles opposés sont proches

Figure 15 : Distance entre toutes les classes

Le niveau de gris de l’unité u de la sous-carte u’ indique la distance entre le représentant de la classe u et celui de la classe u’. La sous-carte 1 correspond à la figure 14. la sous-carte 7 montre l’opposition des angles haut-droite et bas-gauche. Les sous-cartes 24 et 27 montrent que la macro-classe du centre joue un rôle central de la partie gauche de la carte, le bord droit ayant tendance à s’écarter.
24La première approche consiste à rétracter le bord des cellules de chaque unité en proportion de la distance à ses voisines (c’est-à-dire, entre leurs représentants de classe). L’espace blanc entre deux cellules est alors d’autant plus grand que les représentants de classes sont distants. Parmi les 8 points de contraction, ceux qui concernent les 4 voisins en diagonale sont les 4 sommets, ceux qui concernent les voisins latéraux sont les 4 milieux des côtés du rectangle. La figure 13 montre la carte des distances entre classes voisines pour l’exemple sur l’aspect de la peau du visage. On constate une fracture entre la bande de 2 unités du bord droit et le reste de la carte. Cette représentation renseigne sur la structure locale des données, une grande distance pouvant, par exemple, localiser une rupture (fossé) dans la distribution. Par contre, elle ne fournit pas d’indication sur la structure globale, en particulier sur la présence d’un repliement de la surface.
25La carte des distances entre tous les représentants de classe est en fait une représentation de la matrice des distances intra classes (Rousset et Guinot (2001), Rousset et Guinot (2002)). Cette matrice est très grande (dans le cas d’une carte 7x7, elle a 2401 valeurs (49x49)), ce qui la rend inexploitable en général sans un outil approprié. La carte des distances entre tous les représentants de classe permet de l’exploiter en traitant la redondance de la matrice et en faisant ressortir les éloignements et rapprochements majeurs. La figure 14 représente la première ligne de la matrice qui donne les 49 valeurs des distances du centre de la classe 1 à tous les autres centres de classe. Dans l’unité u est représentée la valeur de la distance entre la classe 1 et la classe u par une intensité de couleur (la plus foncée étant la distance la plus élevée). La classe 1 est donc proche des classes colorées de blanc et gris clair et loin des classes gris très foncé. On constate qu’elle est proche de ses voisines (classes 2, 8 et 9) et aussi de l’angle opposé (classes 41 et 49). Elle traduit donc le repliement de la carte dévoilée dans le paragraphe précédent. Les 49 valeurs se résument en cinq zones de proximité et d’éloignement, ce qui constitue un résumé concis de la première ligne de la matrice. Pour traiter toutes les lignes de la matrice, on tient compte du fait que si deux classes i et j sont voisines, alors elles sont proches, respectivement éloignées, des mêmes classes. Par conséquent, les lignes i et j sont similaires et on peut donc les rassembler. Pour le faire, on peut utiliser à nouveau l’organisation en carte comme sur la figure 15 où sont représentées les 49 lignes de la matrice par 49 sous-cartes. Deux sous-cartes voisines contiennent souvent la même information, il convient d’en sélectionner un petit nombre, ce qui est suffisant pour donner la structure d’ensemble du nuage. Par exemple, la sous-carte 1 montre le repliement, la sous-carte 7 montre l’opposition des angles « en haut à droite » et « en bas à gauche». Les sous-cartes 24 et 27 montrent que la macro-classe du centre joue un rôle central pour la partie gauche de la carte, le bord droit ayant tendance à s’écarter. Cette représentation est beaucoup plus lourde que les précédentes, mais elle constitue une description très précise de la structure complète du nuage de points. Ce qui est remarquable ici, c’est que l’utilisateur choisit son niveau de résumé, ou de perte d’information.
26Les cartes d’auto-organisation constituent une alternative intéressante aux modèles classiques pour résoudre les problèmes de représentation et de synthèse. Leur caractéristique majeure est d’être sensible aux petites distances ; c’est-à-dire, aux phénomènes locaux. Elles sont capables de mettre en évidence des tendances, et de s’adapter à des structures non-linéaires. Elles permettent également de percevoir des nuances de comportement chez certaines sous-populations. Sur l’ensemble des exemples traités, elle s’est montrée souple puisqu’on a pu l’utiliser avec plusieurs distances sur des données de tailles parfois très grandes. Son système de représentation permet à la fois de tracer des courbes (dans l’exemple de la consommation électrique, 2922 courbes sont tracées simultanément), de dessiner l’ensemble des camemberts ou histogrammes qui traduisent le croisement de la classification à une variable qualitative, de visualiser les distances intra-classes, etc. Les cartes d’auto-organisation se montrent donc adaptées à l’évolution des besoins en analyse statistique, en particulier pour exploiter des bases de données de plus en plus grandes et chercher, au delà des dimensions principales, l’impact des facteurs secondaires. Sa capacité à mettre en évidence des facteurs, qui n’ont d’effets significatifs que sur une partie de la population, et son potentiel pour ajuster les données par une surface représentée de façon symbolique au lieu d’un plan, rendent cet outil complémentaire aux méthodes classiques. De façon plus générale, c’est parce qu’elle permet d’avoir une approche différente des données, afin de les « voir » autrement, que cette méthode est attractive.



























































